题意:一个$n$个点的完全图,定义$d_x$为生成树上点$x$到根路径上的最小边权。问图$G$的生成树$\sum d_x$最小是多少?
人性化题意:给出$n$个点的完全图,对于完全图中的每个点$i,i$作为终点时,要使其他每个点到点$i$的“距离”和最小,对于每个点都输出这个最小值。 这里的“距离”是指对于其他每个点,那个点到点$i$路径上的最小值。且对于每个点$i$,计算答案时应保证图内每条边的方向一定。
首先可以发现这个路标建出来是一颗树,对于每一个点的贡献是这个点到终点的路径上的最小值。然后有一个十分机智的想法就是对于所有终点,把所有点都连在最短的边的一端,然后另一端连向终点。
然后这个东西显然是假的
不过我们可以考虑对它进行一些微小的修改让它成为正确的。
考虑这个想法的错误之处在于最短边的一端到终点的距离可能很长,所以我们考虑对这个进行计算,最短边的一边到终点路径显然是一条链。
显然这条链的边权只有单调递增时才有意义,因为任意一个破坏单调性的点都可以跟最短边不连接的一端连接,这样显然会更优。
这个过程有点难理解,也比较难实现,所以我们把这个过程想象成一个连边的过程,一开始最短路的一端直接跟终点连接。如下图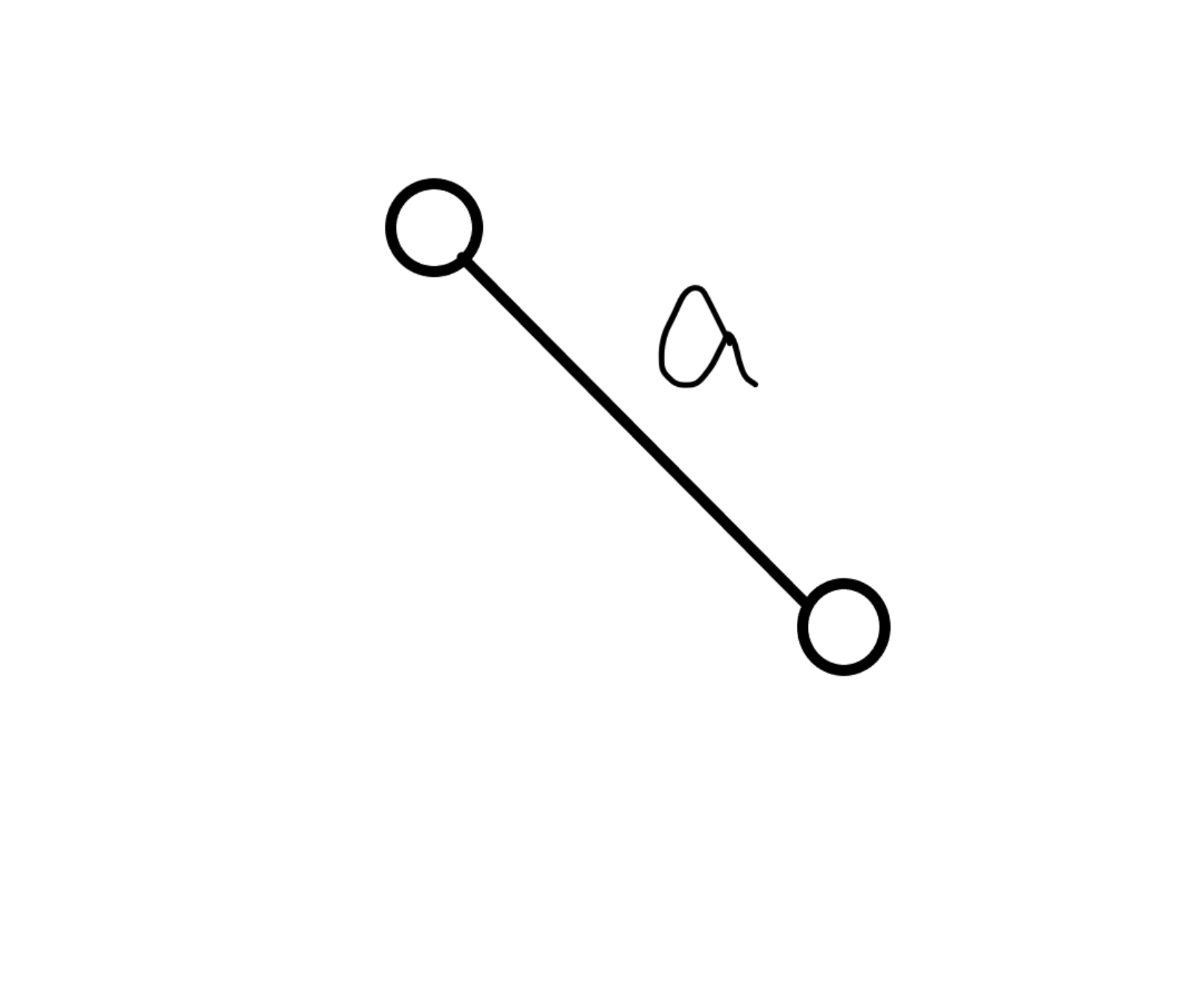
如果要去更新图$1$中的$a$,那么我们必须找到另一个点来松弛它,如图$2$,我们假设$c<b$(因为如果$c>b$,后面最短路操作会更新),那么这些点的总贡献就变成了$2\times c$(显然),因为是一条链,所以我们可以就此跑一遍最短路找出终点到最短边的最小总长度。
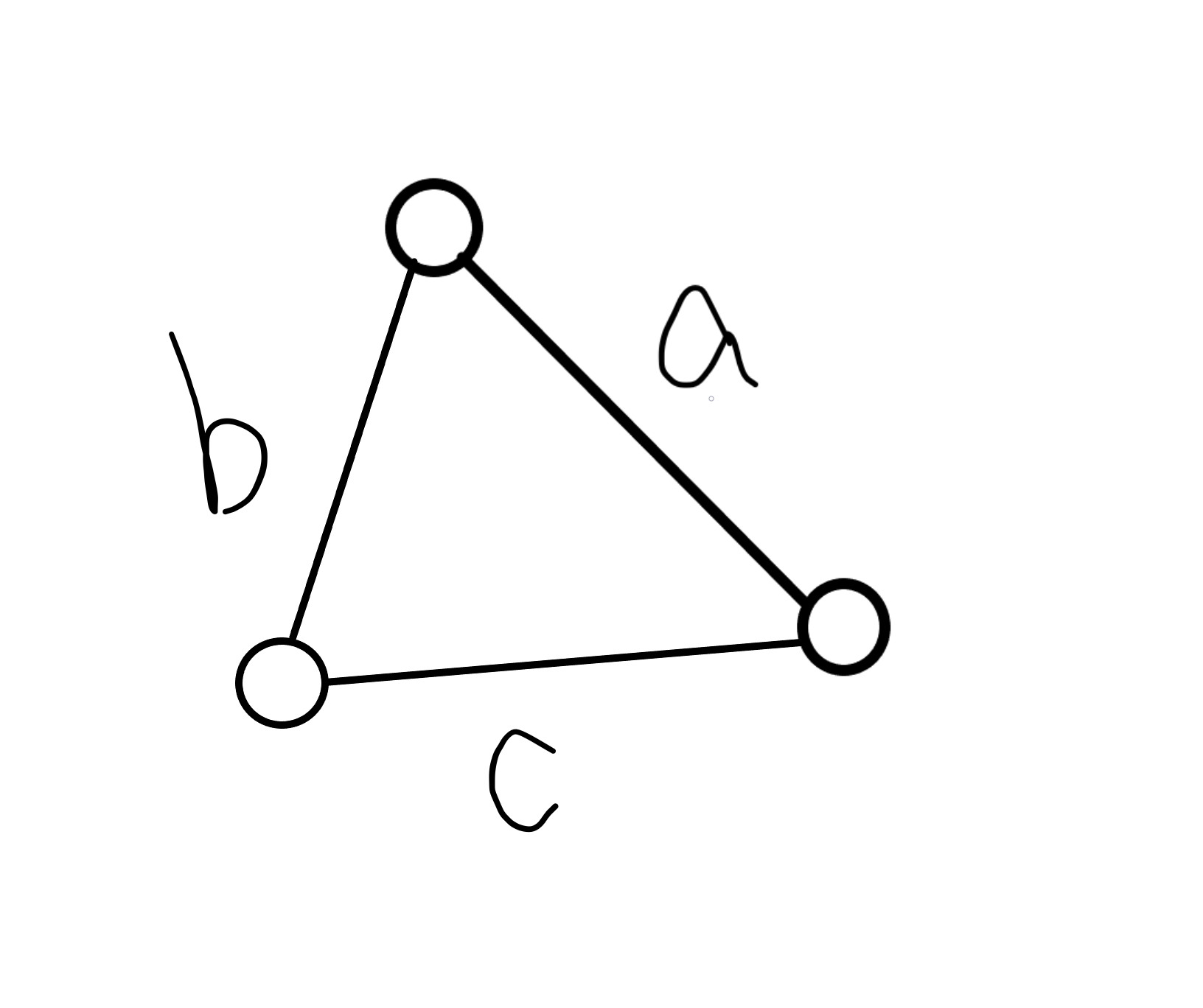
由于过程中维护最短边两端的点各自的个数,我们先将每条边减去最短边的权值,最后在加上最短边权值$\times (n-1)$
怎么计算答案呢?我们设那条链上除终点外有$x$个点,那么那棵树上就有$n-1-x$个点,设最小边长度为$minn$,那么答案为$dis[t]+minn*(n-1-x)$。这个$x$很难计算,考虑消去。即计算$dis[t]$前先对所有边权减去一个$minn$,设新链答案为$dis[t]$,那么答案会变成$(dis[t]+minn\times x)+minn\times(n-1-x)$,即$dis[t]+minn\times(n-1)$,于是$x$就消去了。所以我们计算$dis[t]$即可。
因为要求最优解,我们跑最短路求$dis$(定义见上) 。即向终点直接连边,所以赋为终点与最小点的边权。还有一种状态,即是图$2$的情况,考虑那条链上有$3$个点。设加入的为点$j$,那么链的答案可能为最小点到终点的答案加上$j$到终点的答案,即$a[i][j]\times 2$($a$数组为邻接矩阵,$i$是终点) 最后$dijkstra$松弛即可 (模板) 。
1 |
|